В заключительной части блока по теории вероятностей мы рассмотрим как применять критерии на практике и принцип их работы.
В проверке гипотез мы делаем предположение о распределении данных, и наша задача состоит в том, чтобы определить, содержит ли выборка достаточно информации, чтобы отвергнуть это предположение или нет. Но прямо «в лоб» говорить, что эта гипотеза верная мы не можем:
Чтобы иметь возможность отвергнуть предположение, нам необходимо предоставить альтернативу — иное предположение о распределении данных, относительно которого мы будем решать, отвергать основную гипотезу или нет. Т.е. мы сравниваем обе гипотезы и выбираем ту, которая наиболее вероятна.
Статистический критерий
Обратимся к классическому примеру: предположим, что кто-то подбросил 16 раз монетку, и в 12 случаях она упала орлом вверх. Можно ли считать эту монетку симметричной?
Здесь у нас такое же классическое распределение Бернулли: X1, . . . , Xn ∼ Ber(p).
H0: p = 1/2 (основная или нулевая гипотеза).
H1: p ≠ 1/2 (альтернативная гипотеза).
Правило, позволяющее принять или отвергнуть гипотезу H0 на основе выборки называется статистическим критерием. Сам статистический критерий задается при помощи функции от выборки T(x1, . . . , xn), называемой статистикой критерия. Каждый критерий считает некоторую функцию от данных.
Статистика любого критерия T(x1, . . . , xn) должна обладать двумя основными свойствами:
- При верной H0 статистика T должна принимать умеренные значения, а при неверной H0 — другие, экстремальные.
- При верной H0 статистика T должна иметь известное распределение G0 (называется нулевым распределением), а при неверной H0 — распределение отличное от G0 (возможно, неизвестное).
Проверка гипотезы
Как узнать, что гипотеза H0 верная? В нашем примере в качестве статистики T можно взять
T(x1, . . . , xn) = x1 + . . . + xn.
При верной типичными значениями H0 будут значения, близкими к n/2, а экстремальными — значения, близкие к 0 или n. Итого:
- При верной H0 имеет распределение Bin(n, p) с p = 1/2
- При верной H1 имеет распределение Bin(n, p), но с p ≠ 1/2
Давайте объединим все данные, которые мы имеем:
Выборка: X = (x1, . . . , xn), Xi ∼ F (все случайные величины имеют какое-то конкретное распределение)
Нулевая гипотеза: H0 : F ∈ Ϝ0 (F принадлежит какому-то классу распределений Ϝ)
Альтернативная гипотеза: H1 : F ∈ Ϝ1, Ϝ1 ∩ Ϝ0 = ∅ (два класса не должны пересекаться)
Статистика: T(x1, . . . , xn), T(X) ∼ G0 при H0 (если мы подставляем в статистику подставляем выборку из случайных величин, то статистика H0 должна иметь какое-то конкретное распределение) , T(X) не∼ G0 при H1
Фактический уровень значимости или p-value — это вероятность для статистики T при верной H0 принять значение t = T(x), которое получилось на выборке x = (x1, . . . , xn) или ещё более экстремальное. Иногда p-value называют достигаемым уровнем значимости.
Если p-value будет маленьким, то это означает, что значение, которое будет получено, будет экстремальным, т.е. вероятность получить именно такое значение крайне мало (0,001% например). Это будет свидетельствовать о том, что альтернативная гипотеза (H1) более вероятна (лучше не использовать слово «верна»). Если p-value большое — мы попали в область типичных значений для данной статистики, а значит данные не свидетельствуют против нулевой гипотезы H0 в пользу альтернативы H1
Если для статистики T экстремальными значениями являются большие значения, то это можно записать так:
p(x) = P(T(X) ≥ t | H0).
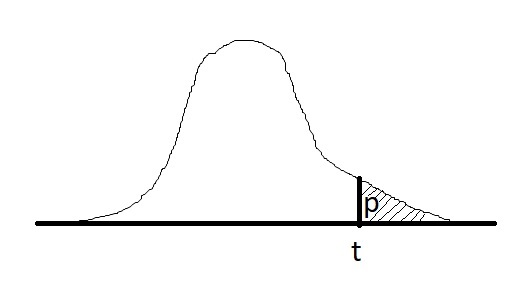
Нулевая гипотеза H0 отвергается при p(x) ≤ α, α — уровень значимости, который мы задаем. Вероятность отвергнуть нулевую гипотезу зависит не только от того, насколько она отличается от истины, но и от размера выборки: по мере увеличения n нулевая гипотеза может сначала приниматься, но потом выявятся более тонкие несоответствия выборки гипотезе H0, и она будет отвергнута.
При помощи инструментов проверки гипотез нельзя доказать, что нулевая
гипотеза верна!
Пример
Ваш закадычный друг утверждает, что у него есть некоторый скилл: он различает чем разбавлен коньяк в коктейле — кока-колой или пепси, и предпочитает только колу. Протестируем его предложим ему выпить n-количестве коктейлей, чтобы проверить: сможет ли он отличить колу от пепси.
Выборка: X = (x1, . . . , xn), где Xi ∼ Ber(p).
Реализация выборки: x = (x1, . . . , xn) — это вектор длины n, где
- 0 — Друг выбрал коктейль с пепси
- 1 — Друг выбрал коктейль с колой
Статистика: T(x1, . . . , xn) = x1 + . . . + xn.
Реализация статистики: t = T(x).
Гипотезы:
- H0: друг не может различить колу от пепси p = 1/2.
- H1: друг может различить колу от пепси, p > 1/2.
Какие значения T считаются экстремальными? При альтернативе H1 экстремальными являются большие значения t (они свидетельствуют против H0 в пользу H1).
Если нулевая гипотеза H0 справедлива и друг не может различить колу от пепси, то
T будет иметь биномиальное распределение Bin(n, 1/2).
Пусть количество коктейлей n = 16, тогда Bin(n, 1/2) будет иметь следующий вид
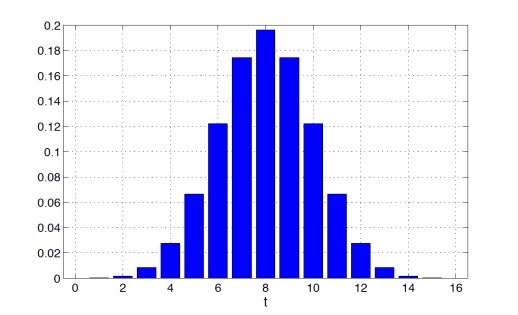
Предположим, что t = 12, то есть в 12 случаях из 16 друг действительно угадал, что в стакане кола. В таком случае p-value будет равен:
P(T(X) ≥ 12 | H0) = 2517 / 65536 ≈ 0.0384
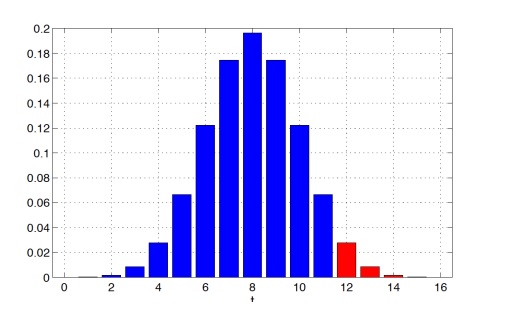
Здесь у нас p-value достаточно мало — это указывает на то, что альтернативная гипотеза (H1) более вероятна, т.е. друг действительно различит колу от пепси
Теперь немного изменим альтернативную гипотезу:
H1: Друг любит определенный коктейль, но неизвестно какой (с колой или с пепси), то есть p ≠ 1/2. При такой альтернативе и большие, и маленькие значения t будут
свидетельствовать против H0 в пользу H1
Предположим (снова), что t = 12, то есть в 12 случаях из 16 друг действительно угадал, что в стакане кола (опять). Тогда p-value будет равен:
P(T(X) ≥ 12 или T(X) ≤ 4|H0) = 5034 / 65536 ≈ 0.0768
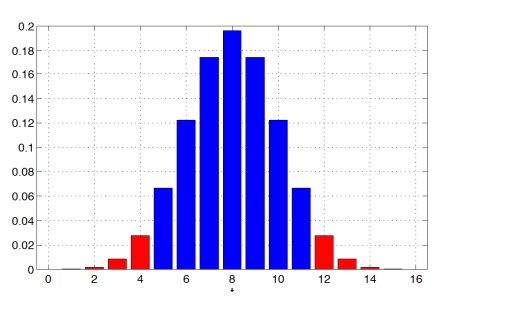
Чем больше, «шире» альтернатива, тем сильнее данные свидетельствуют против нулевой гипотезы H0 (тем больше значений будут считаться экстремальными). С помощью инструментов проверки гипотез нельзя доказать верность нулевой гипотезы в принципе
Критерии согласия
Критерии, которые отвечают на вопрос согласуется ли распределения данных с каким-либо видом распределения, называют критериями согласия.
Пусть нам дана выборка x1, . . . , xn ∼ F, где F — некоторое неизвестное распределение. Давайте рассмотрим критерии согласия, в которых в качестве H0 будем рассматривать гипотезу о принадлежности F какому-то параметрическому семейству, то есть F ∈ Ϝ0. Альтернативой H1 мы будем считать принадлежность F всем остальным распределениям
• H0: F ∈ Ϝ0 (нулевая гипотеза), проверяем гипотезу, что наше распределение F, которое мы не знаем, принадлежит некоторому классу распределений Ϝ0
• H1: F ∉ Ϝ0 (альтернативная гипотеза)
где Ϝ0 — некоторое параметрическое семейство распределений.
Критерии согласия так называются, потому что они отвечают на вопрос, согласуется ли наша выборка с каким-то параметрическим семейством или нет. В англоязычной литературе такие критерии называют Goodness of Fit
Чтобы построить критерий согласия достаточно найти такое свойство, которое будет выполняться для всех распределений в классе и на его основе реализовать статистику. Возьмем за правило, что произвольная гипотеза H является простой, если H : F = F0, то есть гипотеза заключается в равенстве одному конкретному распределению F0. В противном случае мы будем называть гипотезу сложной, т.е. нулевая гипотеза состоит из нескольких распределений (двух и более)
Произведем проверку простой нулевой гипотезы:
- H0 : F = F0 для некоторого конкретного распределения F0.
- H1 : F ≠ F0.
Критерий Колмогорова
Критерий Колмогорова позволяет проверить гипотезу согласия для непрерывного случая и основан на отклонении функции распределения F0 построенной по выборке эмпирической функции распределения
Функцией распределения случайной величины X называют функцию
FX : R → [0, 1], задаваемая следующей формулой
FX(u) = P(X ≤ u)
Значение F в точке u сосредотачивает вероятности всех возможных значений X вплоть до u (включительно).
Основное свойство функций распределения:
Любую случайную величину X можно задать через функцию распределения. То есть по функции распределения можно восстановить распределение случайной величины X:
- В дискретном случае можно восстановить ak и pk (т.е. сможем найти возможные значения и вероятности)
- В непрерывном случае можно восстановить f(u) (т.е. восстановить функцию плотности)
Эмпирическая функция распределения — это функция, которая оценивает истинную функцию распределения выборки F. Она задается формулой
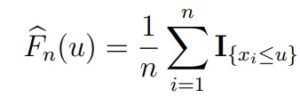
где I{xi≤u} — индикатор события {xi ≤ u} — это функция, которая равна 1, если событие
произошло, и 0 в обратном случае).
Визуально график представляет собой кусочно-постоянную функцию, у которой скачки происходят в точках выборки x1, . . . , xn, а высота скачков равна 1/n. По графику видимо, что истинная функция распределения хорошо аппроксимируется с эмпирической функцией распределения
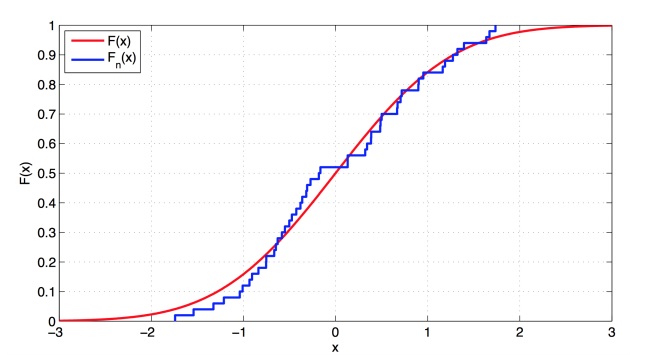
Для выборки достаточно большого размера, эмпирическая функция распределения Fbn(u) не должна существенно отклоняться от истинной функции распределения F.
Теорема (Гливенко-Кантелли)
Если F — это функция распределения элементов выборки, то Fn(u) будет эмпирической функцией распределения, построенной по этой выборке. Тогда, для всех одновременно аргументов функции (u) и при n → ∞
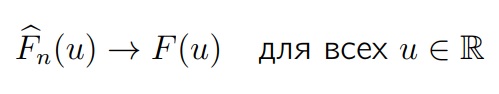
Эмпирическая функция распределения будет стремиться к истинной функции распределения с вероятностью 1
Статистика критерия Колмогорова основана на такой величине максимального отклонения одной функции от другой:
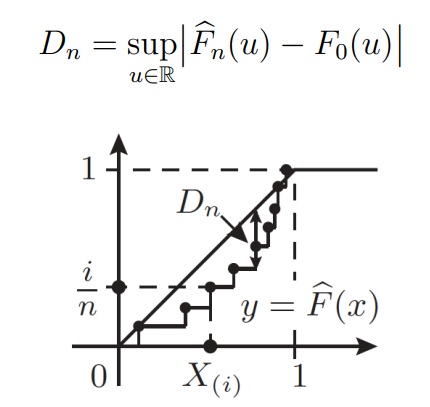
Теорема (Колмогоров)
Пусть верна гипотеза H0, то есть F0 является функцией распределения элементов выборки. Если F0 непрерывна, то, при n → ∞, для любого t > 0
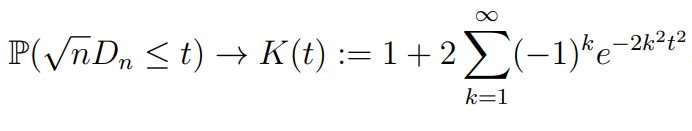
K(t) называется функцией Колмогорова, а соответствующее ему распределение — распределением Колмогорова. Быстрая сходимость к предельному закону позволяет пользоваться этим приближением уже при n ≥ 20. Условие непрерывности функции распределения необходимо
Критерий Пирсона (хи-квадрат)
Критерий Пирсона можно использовать для проверки простой гипотезы согласия в дискретном случае (можно и для непрерывного — но это
Пусть F0 является (пока конечным) дискретным законом, который задается таблицей распределения
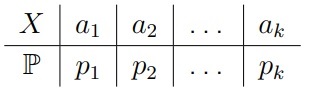
Критерий Пирсона базируется уже на другой статистике — частотах. Статистикой критерия является величина
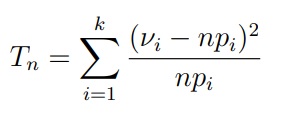
где Vi (греческая буква ню) — количество значений ai в выборке x1, . . . , xn.
Распределением χ2k (хи-квадрат) с k степенями свободы называется распределение случайной величины
Y = χ21 + . . . + χ2k
где x1, . . . , xk независимы и стандартно нормально распределены, то есть Xi ∼ N (0, 1).
Теорема (Пирсон)
Если при n → ∞ распределение статистики Tn сходится к распределению χ2k-1 то нулевая гипотеза верна, т.е. F0 является функцией распределения элементов выборки
Приближение распределения статистики Tn с помощью закона χ2k-1 является достаточно точным при n ≥ 50 и npi ≥ 5 для всех i = 1, . . . , k.
Сложные нулевые гипотезы
Лучше всего проверять гипотезы со специализированными критериями. Поэтому давайте посмотрим на самые чувствительные критерии, которые построены для конкретных семейств распределений.
Проверка экспоненциальности (показательности)
Исключение неизвестного параметра
Положим Sk = X1 + . . . + Xk, k = 1, . . . , n.
Можно доказать, что для экспоненциального распределения вектор (т.е. выборка Xi-тых заменённая на такую) S1/Sn, . . . , Sn−1/Sn, распределен так же, как и упорядоченный ряд из равномерного распределения на [0, 1] размера n − 1.
Данное преобразование сводит задачу к проверке равномерности, которую можно решить с помощью критерия Колмогорова. Но за исключение «мешающего» параметра λ приходится платить уменьшением размера выборки на 1.
Критерий Джини (Gini)
Этот критерий базируется на статистике, а по сути индексу Джини:
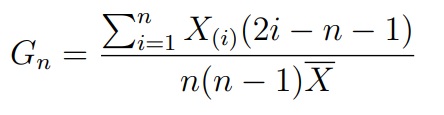
где X(i) — это i-ый элемент в упорядоченной по возрастанию выборке (вариационном ряду). Известно, что при верной H0 величина 12(n − 1)(Gn − 0.5) сходится к нормальному распределению. На этом факте и основан критерий Джини.
Проверка экспоненциальности (показательности)
Для проверки экспоненциальности существует и ряд других критериев (например, Шапиро-Уилка для экспоненциального случая или Андерсона-Дарлинга).
Проверка нормальности
Критерий Шапиро-Уилка (Shapiro-Wilk).
Критерий Шапиро-Уилка базируется на статистике, которая является отношением квадрата линейной оценки стандартного отклонения к смещенной оценке дисперсии:
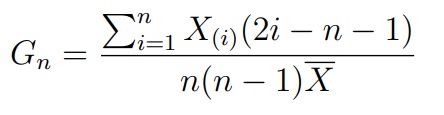
где ai — некоторые константы. При верной H0 распределение SWn является табличным. На этом факте и основан критерий Шапиро-Уилка.
Критерий Харке-Бера (Jarque-Bera). Этот критерий основан на статистике, которая использует выборочные коэффициенты асимметрии и эксцесса:
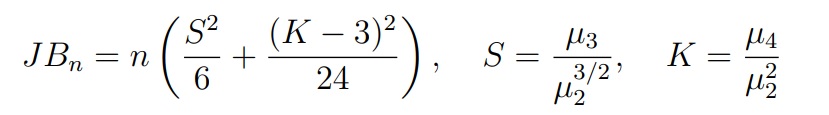
где µk — центрированный выборочный момент порядка k
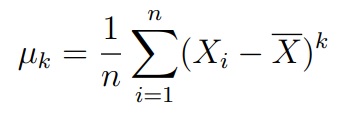
Данная статистика сходится к распределению χ22. На этом факте и основан критерий Харке-Бера.
Квантильный график
До проверки критериев мы делаем визуальный анализ данных. Согласия хорошо проверять с помощью гистограммы. Но по ней довольно сложно судить о правильности убывания хвостов. Чтобы это проверить был придуман квантильный график
Согласие выборки с распределением, которое образовано с помощью сдвига/масштаба, можно проверить визуально с помощью квантильного графика (Q-Q Plot). К таким распределениям относятся: равномерное, экспоненциальное, нормальное и т.д.
На квантильном графике имеются точки, которые должны расположится вдоль некоторой прямой. Если они располагаются как на графике ниже — тогда у нас отличное согласие.
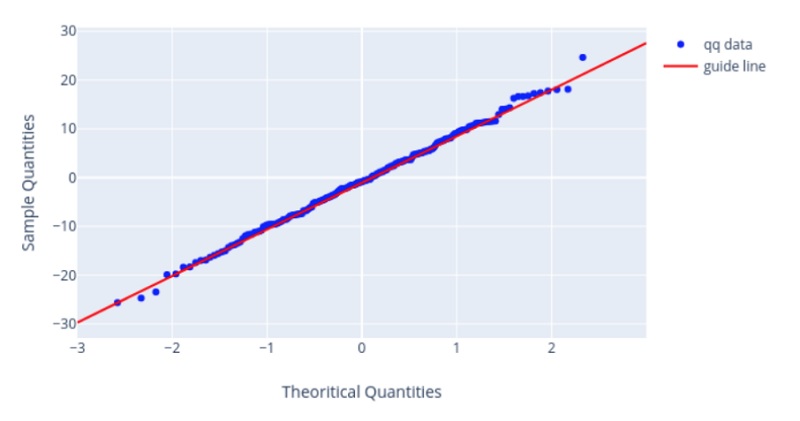
Критерии однородности (A/B тесты)
Критерия однородности, в отличии от критериев согласия, не проверяют согласия выборки с каким-то конкретным распределением, а рассматривают согласие двух выборок, т.е. мы хотим проверить гипотезу, что у них одинаковое распределение.
Например, у нас есть автолюбители, которые предпочитают шины марки А — это будет первая выборка, а есть те, которые без ума от шин марки Б — это будет вторая выборка. Значения в этих выборках — это эффективность работы автомобильных шин (длина тормозного пути, эффективность торможения, шум и т.д.). Требуется выяснить, имеется ли значимое различие эффективности шин А и Б
Есть еще и другой пример: Первая выборка — характеристики до переобувания в зимнюю резину (пусть будут все те же самые, что и выше). Вторая выборка — характеристики после переобувания в зимнюю резину. Требуется выяснить, имеется ли значимое отличие в характеристиках до и после переобувания.
Эти примеры разные в том плане, что в одном случае мы имеем дело с независимым выборкам, а в другом — с зависимыми выборками. Мы будем применять для этих случаев разные критерии.
Параметрические и непараметрические критерии
Параметрические критерии предполагают, что выборка имеет нормальное распределение, т.е. взята из некоторого параметрического семейства распределений. Статистики параметрических критериев более чувствительны к отклонениям от нулевой гипотезы и, в целом, работаю лучше, чем непараметрические (грубо говоря p-value у параметрических обычно ниже, чем у непараметрических критериев)
Но есть одна интересная особенность: непараметрические критерии работают лучше в случае, если совсем немного отходим от нормального распределения. При небольших отклонениях от идеальных условий — они не требуют идеальных условий, например, нормальности данных.
Независимые выборки
Двухвыборочный t-критерий Стьюдента (Уэлча)
Данные критерии основаны на распределении Стьюдента tk с k степенями свободы называется распределение случайной величины, где в числителе стандартная случайная величина, в знаменателе — квадратный корень распределения хи-квадрат с k степенями свободы деленный на количество степеней свободы
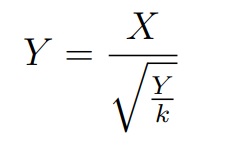
где X ∼ N (0, 1), Y ∼ χ2k и являются независимыми.
Плотность распределения Стьюдента с k степенями свободы:
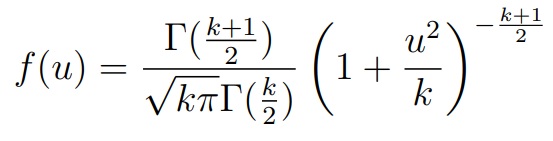
где Γ(u) — гамма-функция Эйлера (специальная функция). Как мы видим, здесь хвосты убывают «тяжелее», чем у нормального распределения
Теорема (Лемма Фишера).Пусть X1, . . . , Xn — выборка из нормального распределения N (µ, σ2). Обозначим среднее арифметическое по выборке и несмещенную оценку для дисперсии:
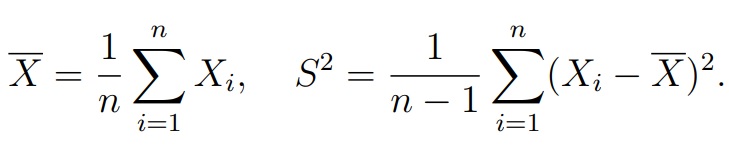
Тогда случайные величины X и S2 независимы
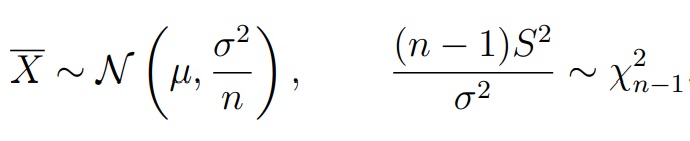
- Выборки: X = (X1, . . . , Xn1), Xi ∼ N (µ1, σ21) и Y = (Y1, . . . , Yn2), Yi ∼ N (µ2, σ22). Выборки могут быть разного размера и имеют нормально распределение. Нюанс: X, Y независимые, σ1 и σ2 неизвестны
- Нулевая гипотеза: H0 : µ1 = µ2
- Альтернатива: H1 : µ1 ≠ µ2 или µ1 > µ2, или µ1 < µ2
- Нулевое распределение: Tn ≈ tk для некоторого k ∈ N
В целом сравнение средних двух нормальных выборок при неизвестных и неравных дисперсиях известна как проблема Беренса-Фишера. При этом рассмотренная аппроксимация (критерий Уэлча) достаточно точна в двух ситуациях:
- Если выборки одинакового размера n1 = n2.
- Если знак неравенства между n1 и n2 такой же, как между σ1 и σ2,
то есть выборка с большей дисперсией имеет больший объем.
Критерий Колмогорова-Смирнова
В качестве первого непараметрического критерия можно использовать модификацию критерия Колмогорова (для непрерывных распределений). Например, две выборки X = (X1, . . . , Xn) и Y = (Y1, . . . , Yn2) с функциями распределения FX и FY соответственно. Обозначим их эмпирические функции распределения и рассмотрим статистику
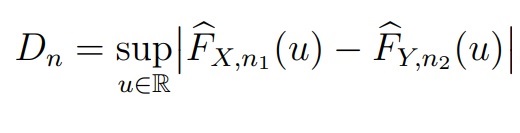
Если FX = FY , то Dn должна принимать малые значения
При выполнении нулевой гипотезы FX = FY , для любого t > 0 выполняется
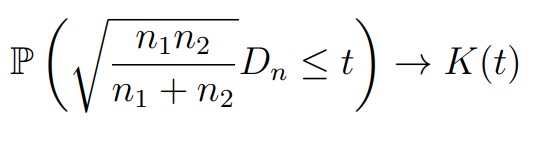
где K(t) — функция Колмогорова (при n1, n2 ≥ 20 аппроксимация является достаточно точной)
- Выборки: X = (X1, . . . , Xn1), Xi ∼ FX и Y = (Y1, . . . , Yn2), Yi ∼ Fy (X, Y независимые; FX, FY непрерывные)
- Нулевая гипотеза: H0 : FX = FY
- Альтернатива: H1 : FX ≠ FY
Критерий Манна-Уитни
Критерий Манна-Уитни (или ранговых сумм Уилкоксона) — еще один непараметрический критерий для проверки гипотезы однородности. Он был предложен Уилкоксоном для выборок одинакового размера. Манн и Уитни обобщили его на случай выборок разного размера.
Напомним, что по любой выборке X1, . . . , Xn всегда можно сопоставить вариационный ряд, то есть упорядочить её по неубыванию:

Рангом наблюдения Xi называется:
- Его позиция в вариационном ряду, если Xi не попадает в связку
- (j1 + j2)/2, если xi попадает в связку от j1 до j2; то есть в связке все
объекты получают одинаковый средний ранг.
Критерий Манна-Уитни основан на следующей статистике Vn:
- Обозначим через Rj ранг порядковой статистики Y(j), j = 1, . . . , m, в вариационном ряду, построенном по объединенной выборке (X1, . . . , Xn1, Y1, . . . , Yn2).
- Положим Vn = R1 + . . . + Rn2
- Выборки: X = (X1, . . . , Xn1), Xi ∼ FX и Y = (Y1, . . . , Yn2), Yi ∼ Fy (X, Y независимые)
- Нулевая гипотеза: H0 : FX = FY
- Альтернатива: H1 : FX ≠ FY
- Статистика: Vn = R1 + . . . + Rn2
- Нулевое распределение: табличное для малых выборок нормальное приближение для больших выборок
Зависимые выборки
Двухвыборочный t-критерий Стьюдента
В некоторых случаях связанные выборки имеют элементы Xi и Yi
соответствуют одному и тому же объекту, но измерения сделаны в
разные моменты (например, до и после применения лекарства).
Размеры выборок в этом случае должны совпадать:
n1 = n2 = n
Рассмотрим выборку, образованную разностями Xi и Yi
Zi = Yi − Xi, i = 1, . . . , n.
Сравнение средних в зависимых выборках ничем не отличается от сравнения среднего разности Zi с нулём.
- Выборки: X = (X1, . . . , Xn1), Y = (Y1, . . . , Yn2), Zi = Yi − Xi и Zi ∼ N (µ, σ2). При этом X, Y зависимые, σ неизвестна
- Нулевая гипотеза: H0 : µ = 0
- Альтернатива: H1 : µ ≠ 0 или µ > 0, или µ < 0
- Нулевое распределение: Tn ∼ tn−1
Далее, чтобы сформулировать непараметрические критерии, возьмем каждое приращение Zi и разложим их на две части:
Zi = θ + εi, i = 1, . . . , n
где θ — систематический сдвиг, который не зависит от человека, а εi — случайные ошибки, включающие в себя влияние неучтенных факторов на Zi
В данных обозначениях нулевую гипотезу H0 можно записать как H0: θ = 0. Мы будем предполагать, что ε1, . . . , εn независимы и имеют непрерывные и разные распределения с равной нулю медианой.
Критерий знаков
Самым простым непараметрическим критерием однородности для двух зависимых выборок является критерий знаков. Статистикой критерия знаков является величина
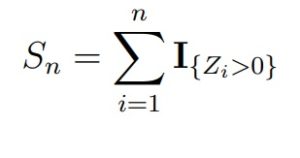
При верной H0 статистика Sn будет иметь биномиальное распределение Bin(n, 1/2), т.е. с успехом 1/2. Для больших n можно использовать сходимость к нормальному закону.
- Выборки: X = (X1, . . . , Xn1), Xi ∼ FX, Y = (Y1, . . . , Yn2), Yi ∼ FY, Zi = Yi − Xi и Zi = θ + εi
- Нулевая гипотеза: H0 : θ = 0
- Альтернатива: H1 : θ ≠ 0 или θ > 0, или θ < 0
- Нулевое распределение: Sn ∼ Bin(n, 1/2)
Критерий знаковых рангов Уилкоксона
Предположим, что случайные величины ε1, . . . , εn имеют одинаковое распределение, симметричное относительно медианы (или же нуля). Условие строгой симметрии относительно медианы является почти столь же нереалистичным, как и предположение, что распределение величин Zi в точности нормально. Как правило, надежно проверить симметрию можно лишь по выборке из нескольких сотен наблюдений
Критерий знаковых рангов Уилкоксона основан на статистике
Wn = R1U1 + . . . + RnUn,
где Ui = I{Zi>0} и Ri — ранги величин |Zi| в ряду |Z1|, . . . , |Zn|.
При верной H0 статистика Wn будет иметь табличное распределение (его можно посчитать явно). Для больших n можно использовать сходимость к нормальному
закону.
- Выборки: X = (X1, . . . , Xn1), Xi ∼ FX, Y = (Y1, . . . , Yn2), Yi ∼ FY, Zi = Yi − Xi и Zi = θ + εi, X, Y зависимые, εi симметрично распределены
- Нулевая гипотеза: H0 : θ = 0
- Альтернатива: H1 : θ ≠ 0 или θ > 0, или θ < 0
- Нулевое распределение: табличное для малых выборок нормальное приближение для больших выборок

