Аналитик данных. Часть 18. Числовые характеристики распределений

Математикам прошлого не сиделось на месте, дай волю, как они опять что-нибудь придумают и накатают очередной, наскоро состряпанный, фундаментальный манифест. А нам потом разгребать. Сегодня это будет математическое ожидание. Как гласит вики, это одно из важнейших понятий в теории вероятностей, означающее среднее (взвешенное по вероятностям возможных значений) значение случайной величины

Математическое ожидание

Для дискретной случайной величины X с таблицей распределения

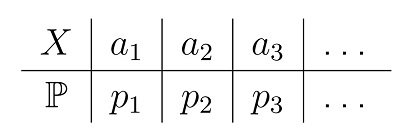
Математическим ожиданием (или средним значением) называется число E[X], которое вычисляется по формуле

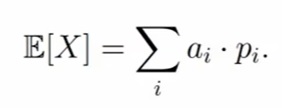
Для непрерывный случайной величины X с плотностью f(u) математическим ожиданием (или средним значением) называется число E[X], которое вычисляется по формуле

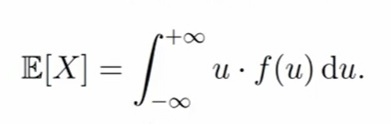
Математическое ожидание тоже подходит для правила перехода из дискретного случая в непрерывному. Сумму меняем на интеграл, a_i меняем на аргумент функции плотности, P_i меняем на f(u)du. Формула следующая:

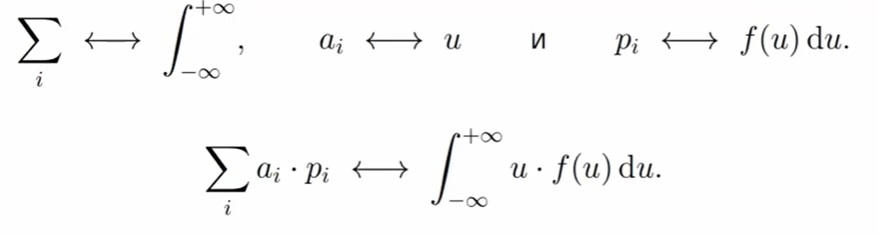
Как интерпретировать математическое ожидание?

Математическое ожидание это, в некотором смысле, среднее значение случайной величины. Окей, мы перемножили значения на вероятности из таблички. Мы получили какое-то число. Допустим, пять. Что оно значит?

Физический смысл: если на отрезке, распределить единичную массу согласно распределению (в дискретном случае поместив в точки a_i массу p_i , а в непрерывном — согласно плотности f), то точка E[X] будет координатой «центра масс» отрезка.

Вероятностный смысл: при многократном повторении эксперимента, ассоциированного с X, среднее арифметическое получившихся значений X1, X2, X3, . . . будет стремиться к E[X], т.е. эксперимент мы повторяем бесконечное количество раз и записываем результат (X1, X2, X3…X_n). Если мы посчитаем среднее арифметическое результата n-экспериментов, то это число и будет математическим ожиданием случайной величины, при n стремящемуся к бесконечности

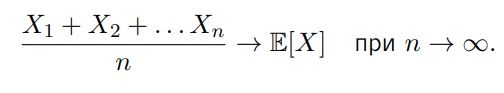
Этот факт называется «Законом больших чисел»

Давайте решим задачку.

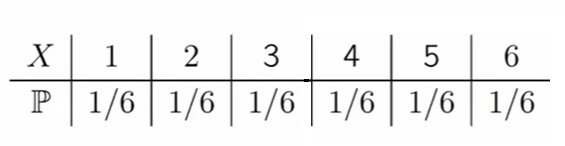
Пусть случайная величина X равна числу очков, выпадающих при одном подбрасывании игральной кости. Найти математическое ожидание E[X]

Как мы помним, вероятность выпадения каждой стороны кубика у нас 1/6

Как мы помним по формуле в начале статьи, нам нужна сумма всех возможных значений случайной величины перемноженных на вероятность их наступления (a_i x p_i):

E[X] = 1*1/6, 2*1/6, 3*1/6, 4*1/6, 5*1/6, 6*1/6 = 21/6 = 3,5

По науке формула будет выглядеть так:

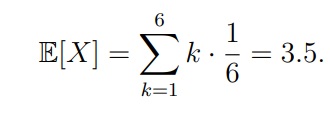
Давайте найдем математическое ожидание (E[X]) равномерного распределения на отрезке от 0 до 1 (Unif[0, 1]). Тут даже без решения понятно, что «центр массы» у нас будет ровно посередине отрезка. С формулой это выглядит так:

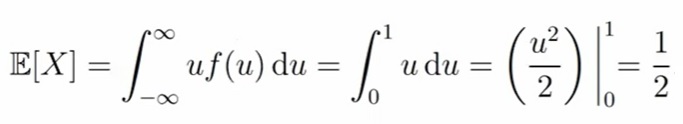
Свойства математического ожидания:

• E[c] = c для любого c ∈ R (математическое ожидание для константы будет равно константе)
• E[cX] = cE[X] для любого c ∈ R (константу можно выносить из мат. ожидания)
• E[X + Y ] = E[X] + E[Y] для любых X и Y (мат. ожидание суммы это всегда сумма мат. ожиданий)
• E[X · Y ] = E[X] · E[Y], если X и Y независимы (мат. ожидание произведений — это произведение мат. ожиданий, если случайные величины независимы)
• Если X ≥ 0, то E[X] ≥ 0 (если случайная величина у нас не отрицательна, соотв. мат. ожидание тоже не отрицательно)

Преобразование случайной величины

Очень часто другие характеристики случайных величин тоже вычисляются как математическое ожидание (не обычное, а от некоторого преобразования случайной величины X). Для этого мы будем использовать произвольную функцию g, т.е. в итоге нам нужно будет найти E[g(X)].

В дискретном случае распределение g(X) будет следующим:

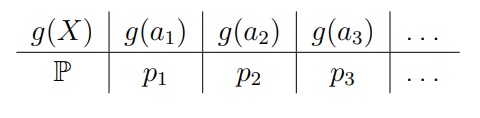
Как это будет выглядеть: если у нас математическое ожидание принимает вид E[x²], то случайная величина X примет значение (а₁)² . Заметим, что вероятность (p) остаётся точно такой же

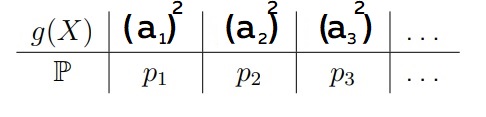
Формула для дискретного распределения:

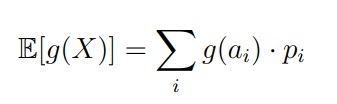
Формула для непрерывного распределения:

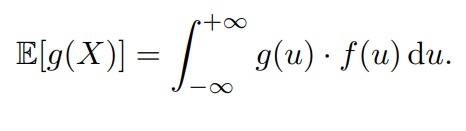
Дисперсия

Если математическое ожидание характеризует среднее значение случайной величины, дисперсия, наоборот, показывает разброс значения случайной величины относительно её математического ожидания. Дисперсия обозначается, как Var(X) и вычисляется по формуле ниже, т.е. дисперсия — это математическое ожидание от формулы случайная величина минус математическое ожидание X в квадрате:

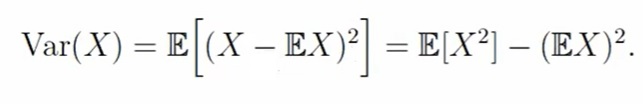
Второй вариант формулы (после второго равно) получается, если применить свойство мат. ожидания. По первому варианту формулы удобней интерпретировать понятие дисперсии. По второму варианту — считать

Стоит заметить, что определение для дискретных и непрерывных распределений — оно одинаковое, однако, мат. ожидание будет считаться в этих случаях по-разному

Как интерпретировать математическое ожидание?

Дисперсия характеризует степень разброса значений случайной величины вокруг её мат. ожидания

Задача

Задача 1. Пусть случайная величина имеет равномерное распределение X ∼ Unif[0, 1]. Найти дисперсию Var(X).

Для решения будем использовать формулу Var(X) = E[X²] − (EX)²

Чтобы найти E[X²], заметим, что это E[g(X)] для g(u) = u² . Из этого следует, что:

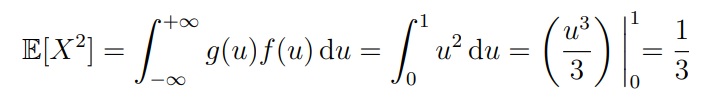
Если E[X] = 1/2, мы получим

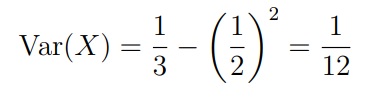
Свойства дисперсии

• Var(c) = 0 для любого c ∈ R (дисперсия константы равна нулю)
• Var(cX) = c² Var(X) для любого c ∈ R (константа тоже выносится с квадратом
• Var(X + Y ) = Var(X) + Var(Y ), если X и Y независимы (дисперсия суммы —
• это сумма дисперсий для независимых случайных величин)
• Var(X + c) = Var(X) для любого c ∈ R (Если мы к случайной величине добавляем константу, то дисперсия никак не учитывает, т.к. это не влияет на сам разброс)
• Var(X) ≥ 0 (дисперсия не может быть отрицательной)

Итого:

Математическое ожидание и дисперсия являются «базовыми» числовыми характеристиками распределений.

Дисперсия для распределение Бернулли: вероятность успеха умноженная на вероятность неуспеха

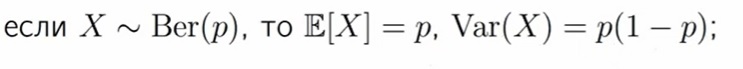
Дисперсия для биномиального распределения: Все характеристики умножаются на n

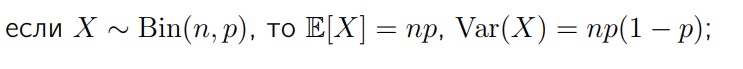
Дисперсия для равномерного распределения: 

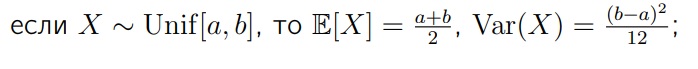
Дисперсия для нормального распределения: Сигма в квадрате

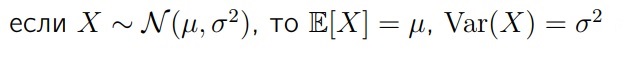
Базовые операции для случайных величин

Центрирование: вычитание из X ее мат. ожидания EX. Это операция позволяет сделать так, чтобы у случайной величины было мат. ожидание, которое равно нулю

E[X − EX] = E[X] − E[X] = 0

Нормирование: деление X на p Var(X). Дисперсию приводим к единице.

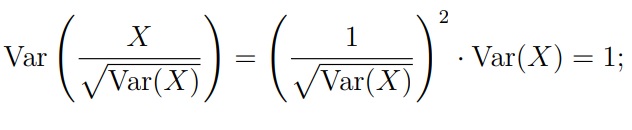
Стандартизация: центрирование + нормирование

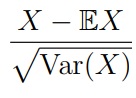
Среднеквадратическое отклонение (или стандартное отклонение) — это квадратный корень из дисперсии случайной величины:

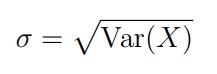
Разделив случайную величину X на σ, мы получим случайную величину с дисперсией Var(X/σ) = 1. Эта операция называется нормировкой.

Характеристики среднего значения случайной величины

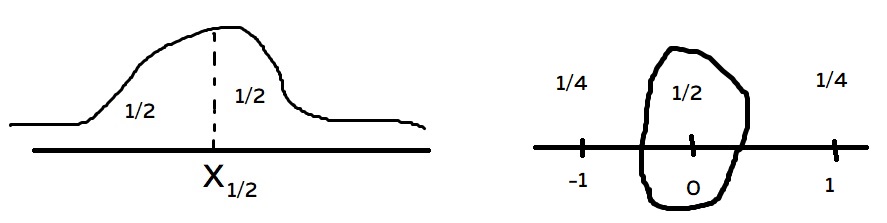
Теоретическая медиана случайной величины X — это число x_1/2, удовлетворяющее неравенствам

Медиана — некоторая точка x_1/2, которая делит функцию плотности пополам с точки зрения  площади под графиком

Теоретическая мода:

• В дискретном случае — значение, которое принимаются с наибольшей вероятностью.
• В непрерывном случае — точка максимума функции плотности

Моменты старших порядков

• E[X^k] — k-ый момент (или момент порядка k)
• E[|X|^k] — абсолютный k-ый момент X
• E[(X − EX)^k] — центральный k-ый момент X
• E[|X − EX|^k] — абсолютный центральный k-ый момент X

Все вышеприведенные моменты характеризуют распределение случайной величины. Они часто появляются в задачах концентрации

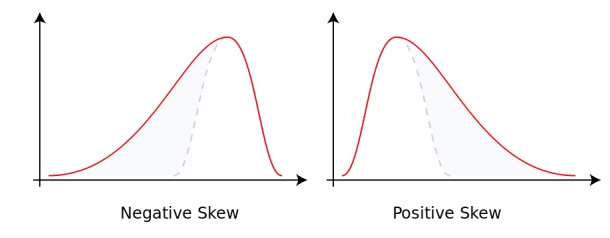
Коэффициент асимметрии (Skewness). Коэффициент асимметрии — величина, характеризующая асимметрию распределения данной случайной величины. Он показывает, если ли у нас скошенность в какую-либо сторону.

Например, вы работаете с выборкой и хотите проверить является ли она «нормальной» —  там могут быть ошибки, но если они распределены нормально, то теоретические свойства модели будут хорошими. Чтобы проверить выборку можно использовать коэффициент асимметрии.

Если значение γ₁ по модулю большое, то в выборке есть скошенность. Если значение близко к нулю, то ваша выборка нормальная.

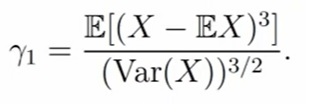
γ₁ — нормированный центральный момент порядка 3

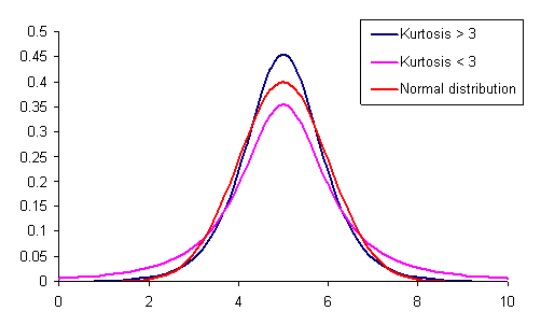
Коэффициент эксцесса (Kurtosis)  — величина, которая характеризуют кривизну функции плотности около точки максимума. По научному — это мера остроты пика плотности
распределения случайной величины.

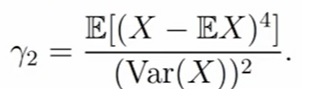
γ₂ — нормированный центральный момент порядка 4. Если мы получим коэффициент эксцесса больше трёх, то это означает, что около точки максимума функция плотность имеет более острый пик, если меньше — функция плотности имеет меньшую кривизну