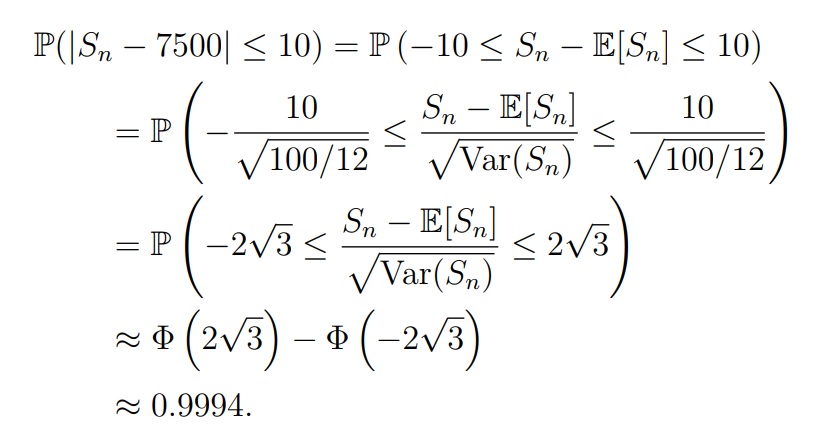Аналитик данных. Часть 19. Суммы случайных величин. Предельные теоремы. Неравенства концентрации

Часто в практических задачах возникает необходимость рассмотрения нескольких случайных величин одновременно: какова вероятность, что в Магните будет акция не только на дошик, но и на пельмени?

Распределение суммы случайных величин

Пусть даны две независимые случайные величины X и Y. Что такое, в принципе, расчёт распределения сумм? Это означает какие значение сумма принимает и с какой вероятностью:

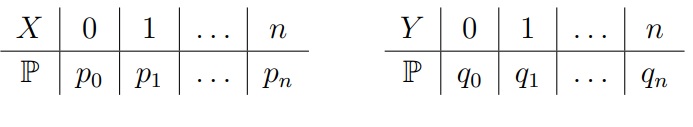
Минимальное значение, которое мы можем получить — 0, максимальное — 2n

Всё сводится к формуле полной вероятности — пробегаемся по всем значениям одной случайной величины. Узнав её, мы восстанавливаем значение второй, зная, что в сумме они дадут k. Вероятность получить значение k складывается как сумма всех значений вероятности X от 0 до k, при этом Y будет k-j

Например, нам нужно узнать  чему будут равны вероятности P(X + Y = k), где
k — любое целое число от 0 до 2n (сумма не превышает 2n)? Распределение суммы X + Y можно найти так: для 0 ≤ k ≤ 2n

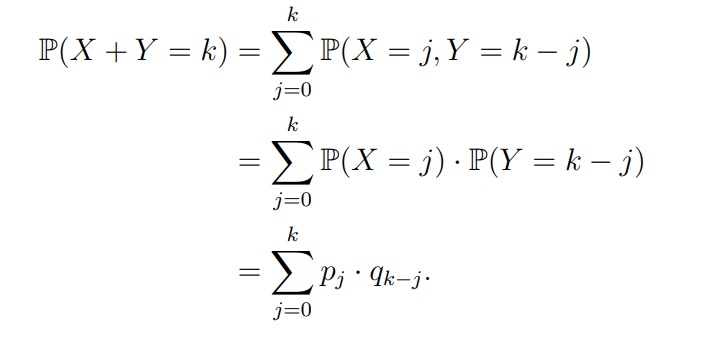
Формула в дискретном случае

Формула распределения сумм в дискретном случае называется дискретной свёрткой. Чтобы найти вероятности P(X + Y = c) для всех возможных значений c ∈ R нужно понять, при каких a_i и b_j получается a_i + b_j = c и просуммировать соответствующие произведения вероятностей p_i· q_j

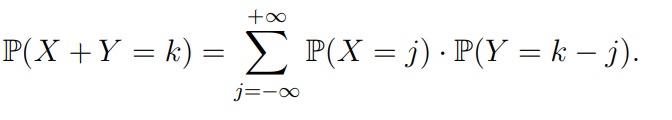
Формула в непрерывном случае

Формула распределения сумм в дискретном случае называется непрерывной свёрткой.

Если две случайные величины независимые, то плотность суммы вычисляется по след. формуле (сумму меняем на интеграл, вероятность меняем на плотность умноженную на dz). Пусть X имеет плотность fX(u), а Y — плотность fY (u).

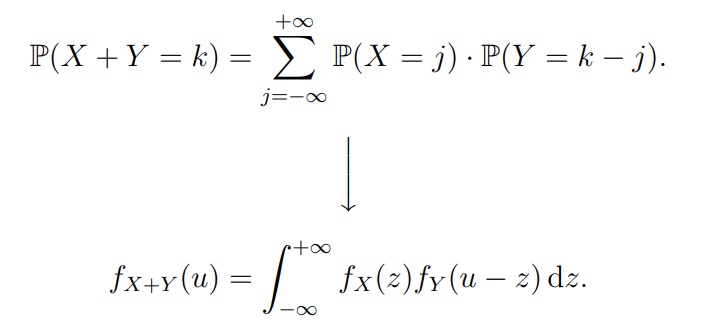
В непрерывном случае, для подсчета суммы двух случайных величин их нужно перемножить и проинтегрировать. Поэтому данные формулы довольно сложно использовать на практике, т.к. их вычислительная сложность растёт с ростом количества слагаемым.

Неравенства концентрации

Неравенства концентрации — это некоторые неравенства, которые позволяют оценить вероятность событий для случайной величины, если мы не знаем её распределения или оно считается очень сложно. Неравенства концентрации — оценка вероятности P(X ∈ A) с помощью числовых характеристик X.

Теорема (Неравенство Чебышёва)

Давайте возьмем произвольную случайную величину, неважно какая у неё таблица распределения или функция плотности, но мы точно знаем, что у неё конечная дисперсия. В таком случае выполняется подобное неравенство: случайная величина примет «плохие» для себя значения (сильно отойдет от своего математического ожидания) на уровень больше, чем t

Пусть X — произвольная случайная величина и Var(X) < ∞. Тогда для любого t > 0

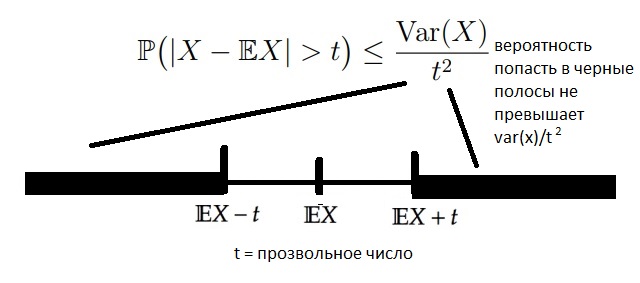
Вероятность, которую мы оценивали в неравенстве Чебышёва можно оценить по-другому, например

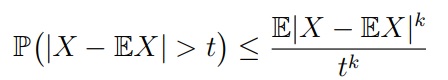
Закон больших чисел

Пусть X1, X2, X3, X_n — независимые одинаково распределенные случайные величины. Например, наша месячная зарплата в день. Определим сумму первых n-членов последовательности: S_n = X1 + . . . + Xn.

Так как у нас случайные величины распределены равномерно, у них совпадает мат. ожидание и дисперсия. Поэтому пусть µ = E[X_n] и σ² = Var(X_n) < ∞.

Таким образом, Теорема (Закон больших чисел, ЗБЧ)  любого t > 0: Вероятность (P) среднего арифметического (S_n/n) отклонится от мат. ожидания на уровень больше чем t сводится к нулю при n -> ∞

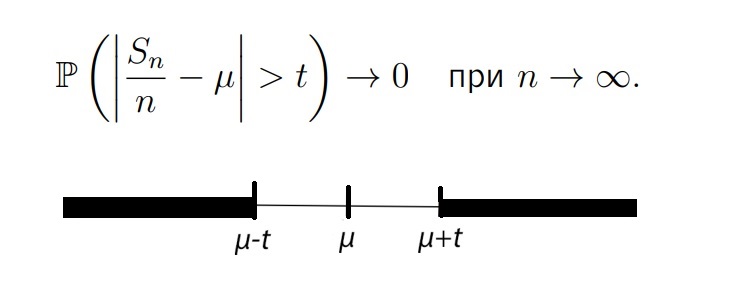
Закон больших чисел можно интерпретировать по-другому: «S_n / n сходится к u по вероятности»

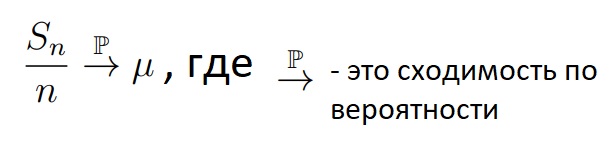
Доказательство закона больших чисел

Найдем мат. ожидание S_n/n. Здесь мы воспользуемся лайфхаком: константу можно вынести из под мат. ожидания (1/n). Еще одно свойство: мат. ожидания суммы — это сумма мат. ожиданий:

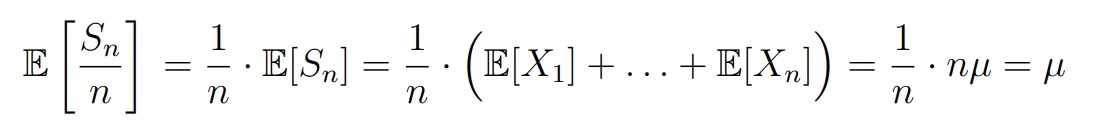
Далее найдем дисперсию. Здесь мы тоже можем вынесем константу, только с квадратом (1/n²)

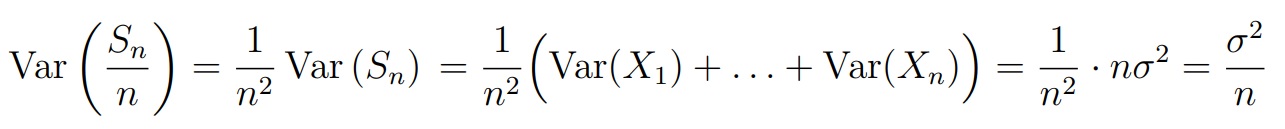
По неравенству Чебышёва:

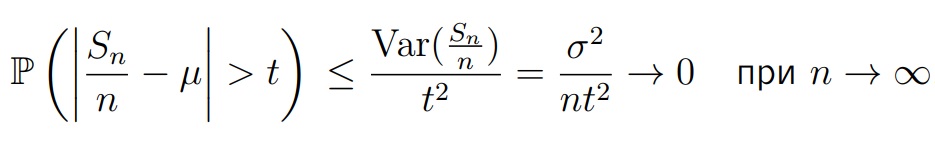
Центральная предельная теорема. Концентрация сумм

Давайте посмотрим, как ведут себя отклонения, если S_n / n сходится к u по вероятности?

Центральная предельная теорема (ЦПТ) — любые вероятности (вероятность попасть в отрезок от a до b) для S_n после вычитания мат. ожидания E[S_n] и деления на корень дисперсии, т.е. стандартизации, будут сходиться при n -> ∞ к таким же вероятностям, где мы стандартизованную величину (то, что у нас в скобочках) заменим на Z, где Z ∼ N (0, 1).

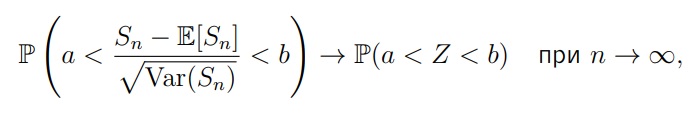
Стандартизация S_n / n и S_n дает одинаковый результат:

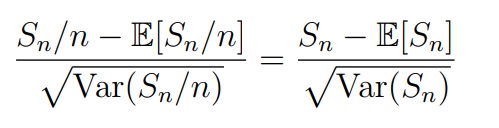
Стоит учесть, что вероятности P(a < Z < b) для Z ∼ N (0, 1) считаются с помощью функции распределения Φ(u) = P(Z ≤ u) по формуле P(a < Z < b) = Φ(b) − Φ(a).

Решение задач #1

В Уездном городе в месяц рождается 10 000 детей. Оцените с помощью неравенства Чебышёва и центральной предельной теоремы вероятность того, что число мальчиков, среди новорожденных будет отличаться от 5000 не более, чем на 100.

Что мы знаем? У нас есть случайные величины X₁….X_n. Все они из распределения Бернулли с вероятностью успеха р, в нашем случае это  ∼ Ber(1/2). Количество экспериментов n = 10 000.

Как мы знаем: S_n = X₁ + . . . + X_n.Таким образом, S_n — это и будет количество мальчиков. Т.е. по условиям задачи нам нужно оценить вероятность того, что этот параметр будет лежать в диапазоне от 4900 до 5100. Сначала найдем мат. ожидание и дисперсию S_n

Мат. ожидание: E[S_n] = E[X₁ + . . . + X_n] = n · E[X₁] = np = 5 000

Дисперсия: Var(S_n) = Var(X₁ + . . . + X_n) = n · Var(X₁) = np(1 − p) = 2500 (дисперсия одного слагаемого p(1-p))

По неравенству Чебышёва: В оригинальной трактовке неравенства мы отклонялись «больше, чем на уровень». Сейчас у нас ситуация обратная — нам надо найти «не больше, чем на уровень», поэтому мы переходим к дополнительному событию (добавляем 1- к P(|S_n − E[S_n]| > 100 и Var(S_n)/100²), соотв. меняется и знак неравенства

По неравенству Чебышёва вероятность отклониться от мат. ожидания не больше, чем на 100 —  она больше или равна 75 процентам, т.е. в трёх случаях из четырёх это событие будет происходить.

По центральной предельной теореме: Сразу упрощаем внешний вид для удобства, т.е. запишем вероятность как P(4900 ≤ S_n ≤ 5100). Далее переходим к нормальному распределению:

 

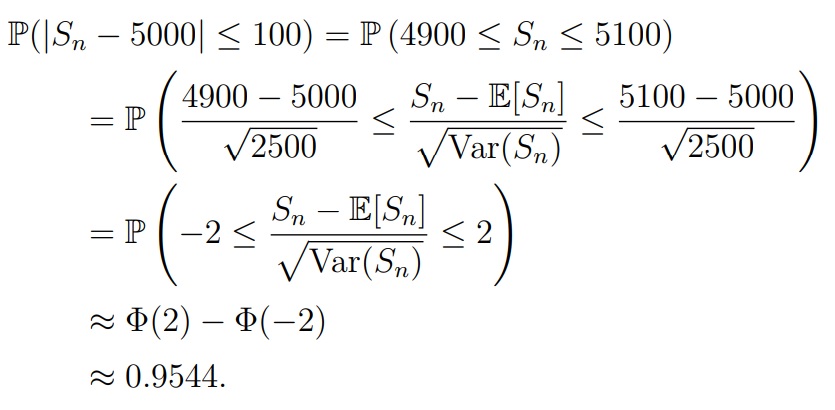
Решение задач #2

Вы — фанат прогулок. Ваши шаги — независимые одинаково распределенные случайные величины, равномерно распределенные на [70, 80] см. С какой вероятностью вы за 10 000 шагов пройдете расстояние, отличное от 7.5 км. не более, чем на 10 м.?

Небольшая хитрость данной задачи состоит в том, что у неё разные единицы измерения. Для удобства приведём все значения в метры: пусть X₁, . . . , X_n ∼ Unif[0.7, 0.8] (метров), n = 10 000, в то время как сумма последовательностей у нас S_n = X₁ + . . . + X_n

Как обычно, сначала находим мат. ожидание и дисперсию:

E[S_n] = E[X₁ + . . . + X_n] = n · E[X₁] = n ·(0.8 + 0.7/2) = 7 500

Var(S_n) = Var(X₁ + . . . + X_n) = n · Var(X₁) = n · (0.8 − 0.7)² / 12 = 100 / 12

По неравенству Чебышёва:

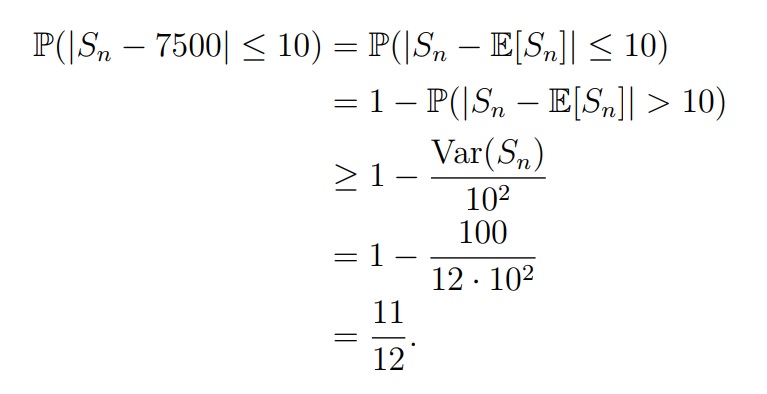
По центральной предельной теореме: