Когда мы хотим пересчитать вероятность некоторого события при условии, что какое-то другое событие произошло, мы используем условную вероятность.
Условная вероятность
Чтобы понять, что это такое, рассмотрим один пример:
Игральная кость подбрасывается один раз. Известно, что
выпало (строго) больше трёх очков. Какова при этом вероятность
того, что выпало нечётное число очков?
Мы знаем, что у игральной кости 6 граней, поэтому вероятность выпадения каждой цифры — 1/6, так же по условиям задачи у нас результат строго больше трёх.
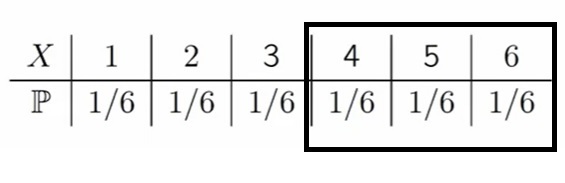
Нам нужна условная вероятность, того, что выпало нечетное число очков. Давайте рассуждать. Нечетное число из условия «больше трёх» у нас только одно — пятёрка.
Когда мы считаем условную вероятность (всю вероятностью массу значений), вероятности которые уже не происходят надо перераспределить на значения, которые происходят, иначе в итоге мы не получим единицу в итоге. Поэтому, мы переносим с 1,2,3 значения 1/6 к 4,5,6. А значит под цифрами 4,5,6 будут значения 1/3.
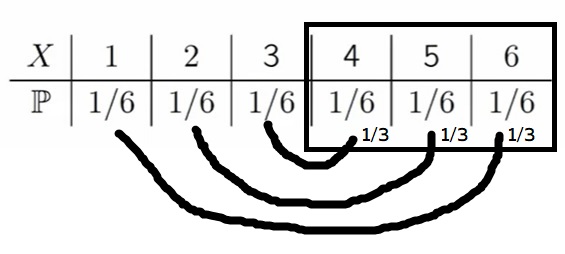
Правильный ответ: 1/3.
Итак, условной вероятностью события S при условии, что произошло событие
H, называется число
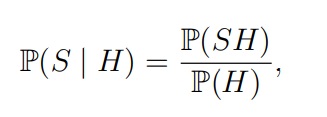
Прямая черта | означает «при условии». SH = S⋂H — пересечение событий S и H (событие, когда S и H происходят одновременно, т.е. исходы есть в обоих событиях).
На примере задачки с игральной костью:
- событие S {x — нечётное}
- событие H {x>3}
Давайте посмотрим на числитель формулы — P(SH), т.е. там мы должны прописать вероятность, где выполняются два условия одновременно, т.е. больше трёх и нечётное — это пятёрка, соотв. её вероятность 1/6 — записываем
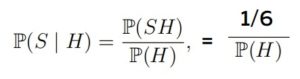
Событие H — это у нас числа больше трёх. Это 4,5,6. Их вероятность (1/6+1/6+1/6) равна 1/2 — так и запишем:
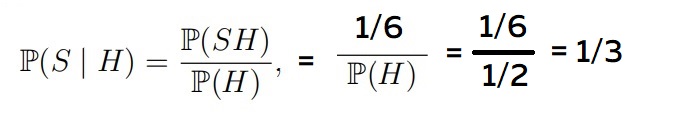
Результат этого вычисления 1/3
Важный момент: Вероятность P(H) не должна быть равна нулю (т.к. деление). В случае P(H) = 0 будем считать, что условная вероятность P(S | H) не определена.
Формула полной вероятности
Здесь мы тоже обратимся к примеру. Допустим, вы с братюней играете в CS 1.6. Вас двое стрелков и каждый с какой-то степенью вероятности делает хэдшот. Вы — про игрок, ваш друг — нуб. Т.е. вероятность сделать хэдшот у вас будет разная, но всё равно, так или иначеЮ попасть в голову есть у обоих
Чтобы выбрать, кто из вас стреляет — вы подкидываете монетку, т.е. шанс, что каждый будет стрелять прямо сейчас — 1/2.
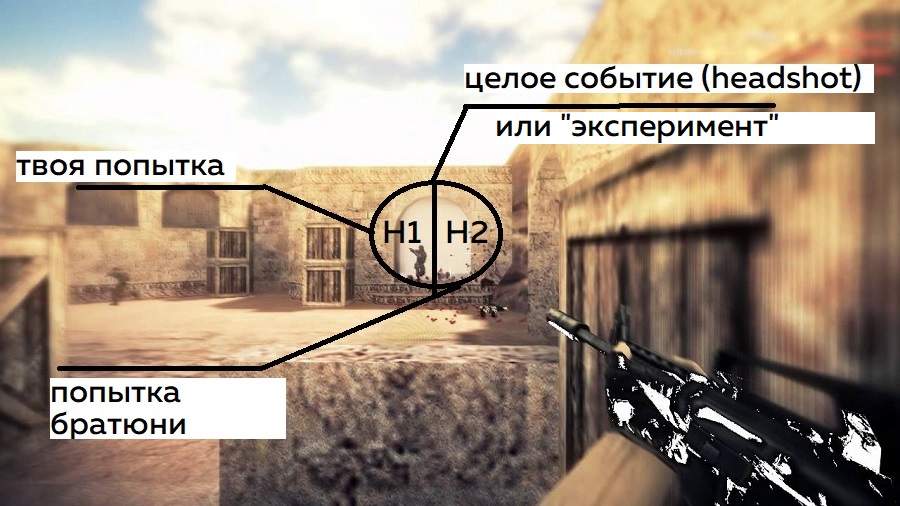
Таким образом, вы целое событие (эксперимент) разбили как бы на два (событие внутри события, да). Твоя попытка (H1) — одно событие, попытка братюни (H2) — другое событие.
Разбиением называется конечный или счётный набор попарно
непересекающихся событий H1, H2, . . . , объединение которых равно
тождественному событию (множеству всех возможных результатов
эксперимента).
При этом не факт, что и ты, и он попадете в голову сопернику, вы ведь можете промазать. Вероятность успеха мы обозначим S
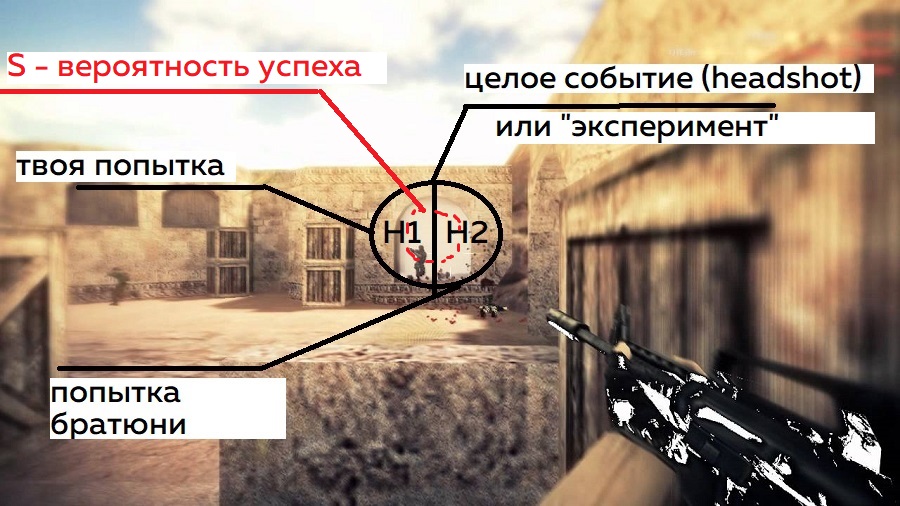
Таким образом, чтобы посчитать общую вероятность успеха (S) вам нужно посчитать вероятность, что будет стрелять первый игрок (H1) и попадёт по мишени, и вероятность того, что будет стрелять второй игрок (H2) и тоже попадёт по мишени. Такие события (ваши выстрелы в данном случае), обычно называются гипотезами
Обычно для некоторого события S можно вычислить P(S | Hi) и P(Hi). Чтобы было понятно, переведём в наш пример: P(Hi) — это вероятность того, что будет стрелять либо первый игрок, либо второй (подкидывание монетки), P(S | Hi) — условная вероятность, что произошло событие S (кто-то из вас попал) при условии выполнения гипотезы
Разложим событие S на кусочки:
S = S ∩ (H1 ∪ H2) = S∩H1 ∪ S∩H2
Теперь перейдем непосредственно к формуле полной вероятности
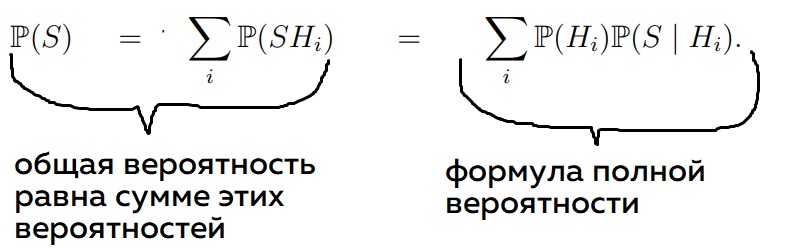
Давайте решать задачу. Вы, как отец в КС, выдаете хэдшот с вероятностью 1 (предположим, вы всегда попадаете), ваш друг нуб попадает в голову с вероятностью 10-5 .С какой вероятностью в результате эксперимента пуля попадет в мишень? Делаем разбиение по событиям (гипотезам)
- S = {попадание в голову, хэдшот} — это как раз то, что мы ищем
- H1 = {Стреляет первый игрок, вы}
- H2 = {Стреляет второй игрок, братюня}
По условиям, у вас равные шансы на выстрел: P(H1) = P(H2) = 1/2
Подставляем данные по формуле полной вероятности: P(S) = P(S | H1)P(H1) + P(S | H2)P(H2)
Если в числом значении, это будет 1 * 1/2 + 10-5 *1/2 = 1 + 10-5 / 2 — такова вероятность, что эксперимент завершится удачей (будет хэдшот)
Формула Байеса
Формула Байеса позволяет переоценить вероятности гипотез после того, как получено знание о результате эксперимента. Если перенести эту формулировку на нашу задачу, то можно представить следующую ситуацию:
Кто-то из вас сделал попал по мишени, эксперимент завершился удачей. Но вам нужно выяснить, кто из вас конкретно сделал этот хэдшот
Т.е. по факту мы меняем события: P (H1 | S), т.е. мы считаем вероятность того, что стрелял первый игрок при условии, что он попал в мишень). Да, при условии, что вы попадаете всегда в цель, а ваш братюня стреляет в молоко, скорее всего, это сделал первый игрок, но всё равно нельзя исключить возможность, что это попал второй игрок. Для этого нам и понадобится формула Байеса
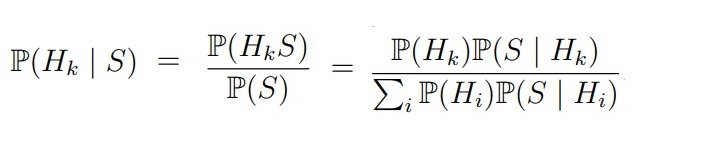
Вероятность одного события делим на вероятность всех событий
Теперь мы можем решить задачу. Вероятность для первого стрелка ≈ 0,99999:
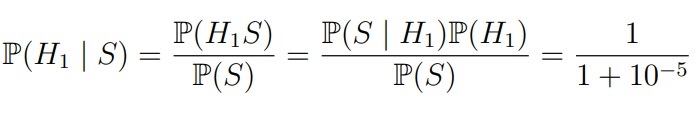
Для второго 0,000001:
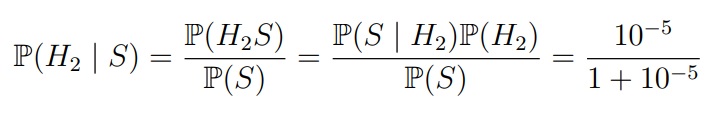
Еще одна задачка
Предположим, что некий тест на какую-нибудь болезнь имеет вероятность успеха 95%; то есть 5% — это вероятность ошибки теста. Предположим также, что болезнь очень распространена и имеется у 1% респондентов. Пусть теперь некий человек получил позитивный результат теста. С какой вероятностью этот человек действительно болен?
Чтобы упростить решение задачи, давайте выпишем все события, которые в ней описаны:
- S = {тест оказался положительным}
- H1 = {человек болен}
- H2 = {человек не болен}
Теперь распишем известные нам вероятности:
- P(H1) = 0,01 — вероятность, что человек болен (т.е.1% по умолчанию)
- P(H2) = P(H2) — 1 — P(H1) = 0,99 — вероятность, что человек не болен (99% людей в мире здоровы)
- P(S1H1) = 0,95 (тест оказывается положительным и человек действительно болен)
- P(S1H2) = 0,05 (вероятность ошибки теста).
Итак, что мы ищем, мы ищем вероятность того, что человек болен при условии, что тест оказался положительным — P(H1|S).

Парадокс Монти Холла
Самый популярный парадокс, связанный с условной вероятностью. Если быть точнее — это задача в теории вероятностей, решение которой, на первый взгляд, противоречит здравому смыслу. Эта задача не является парадоксом в узком смысле этого слова, так как не содержит в себе противоречия, она называется парадоксом потому, что её решение может показаться неожиданным. Звучит она так:
Представьте, что вы стали участником игры, в которой вам нужно выбрать одну из трёх дверей. За одной из дверей находится автомобиль, за двумя другими дверями — козы. Вы выбираете одну из дверей, например, номер 1, после этого ведущий, который знает, где находится автомобиль, а где — козы, открывает одну из оставшихся дверей, например, номер 3, за которой находится коза. После этого он спрашивает вас — не желаете ли вы изменить свой выбор и выбрать дверь номер 2? Увеличатся ли ваши шансы выиграть автомобиль, если вы примете предложение ведущего и измените свой выбор?

На самом деле, решение задачи сводится к тому, что ДА, надо соглашаться на предложение ведущего. Если кратко:
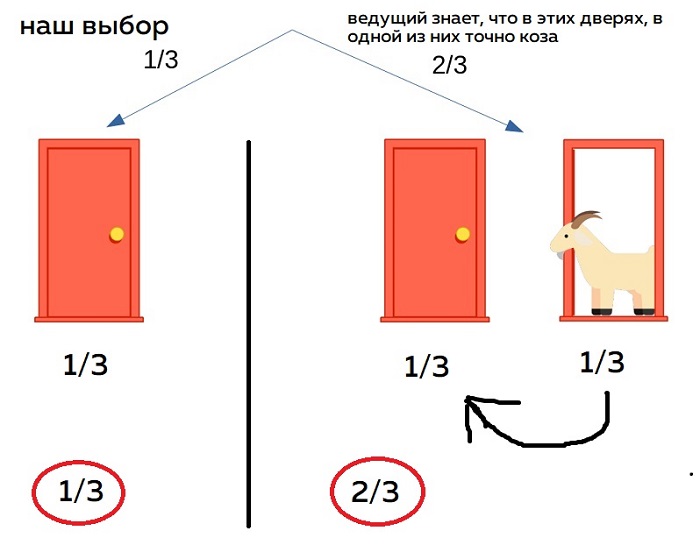
Подробное решение можно почитать здесь.

