Теория вероятностей изучает закономерности, возникающие в случайных
экспериментах (точнее, в их математических моделях). Случайные эксперименты в теории вероятностей моделируются с помощью объекта «случайная величина«. Это вообще центральный объект в теории вероятности. И это немного сложнее, чем подбрасывание монетки. Орёл или решка?
Случайные величины
Случайная величина — это функция, которая каждому возможному исходу в эксперименте ставит в соответствие действительное число. Можно понимать случайную величину как «кодирование» исходов эксперимента. Иными словами, с помощью случайной величины мы моделируем случайный эксперимент, ведь логично, что в теории вероятностей мы изучаем вероятность наступления какого-либо события
Нас будет интересовать множество значений случайной величины и с какими вероятностями она принимает возможные значения, т.е. мы будем говорить о вероятности событий, которые связаны со случайными величинами. Например, если X — случайная величина (будем обозначать большими латинскими буквами), то нас могут интересовать вероятности событий.
Как записывается событие
- {X = a} для некоторого a ∈ R — (в фигурных скобках записано, что случайная величина принимает какое-то значение), a — любое произвольное действительное число, ∈ — принадлежит, R — множество действительных чисел (дробные, иррациональные в т.ч.)
- {X < a} для некоторого a ∈ R
- {a ≤ X < b} для некоторых a, b ∈ R, a < b (из промежутка для каких-то чисел a и b)
В самом общем виде любое событие можно записать так: {X ∈ A} для некоторого подмножества A ⊂ R
Классификация случайных величин
Можно (нужно!) классифицировать случайные величины по мощности их множества значений
Дискретные случайные величины имеют конечное или счетное
множество значений. Примеры: {1, . . . , n}, N, Z. Это в случае, если бесконечность счетная, т.е. мы можем пересчитать элементы этой бесконечности. Это счетное множество. Например, N — все натуральные числа (от 1 до бесконечности). Z — все целые числа и так далее
Непрерывные случайные величины имеют несчетное множество
значений. Примеры: [0, 1], R. Это бесконечность на стероидах, т.е. еще «большая» бесконечность, чем обычная бесконечность, т.к. мы не можем пересчитать её элементы. Например, любой отрезок, скажем от 0 до 1, т.к. в нём присутствуют иррациональные числа (дроби, корни), которых очень много. И процесса пересчёта не существует — их будет бесконечно много
Дискретные случайные величины
Исходы дискретной случайной величины мы можем посчитать — мы можем приписать вероятности всем возможным значениям случайной величины. На примере монетки: значение ноль (решка) принимается с вероятностью 1/2, соответственно значение единица (орёл) принимается так же с вероятностью 1/2.
Чтобы задать распределение дискретной случайной величины, необходимо всем возможным значениям этой случайной величины приписать вероятности. Например:
- Перечислить возможные значения a1, a2, a3, . . .;
- Задать действительные числа p1, p2, p3 при условии
1) Вероятности не могут быть отрицательными (неотрицательность)
pi ≥ 0
2) Сумма всех значений вероятностей должна быть равна единице (нормировка)
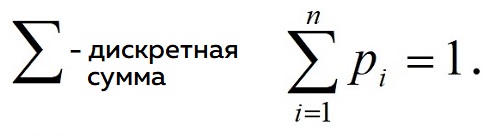 .
.
Это удобно делать с помощью таблицы распределения вероятностей X, где X — возможные значения случайной величины, P — вероятность каждого значения
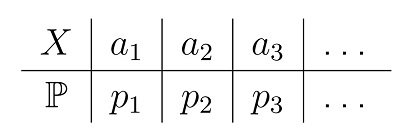
Если задано распределение дискретной величины, то вероятность любых событий можно посчитать по формуле:
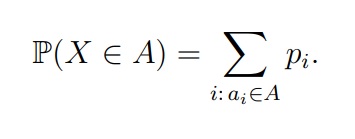
Читается это так: чтобы просчитать вероятность (P) любого произвольного события (X∈ A), нужно взять исходы, которые входят в множество А (ai ∈ A) и для этих индексов (i) просуммировать соответствующие вероятности Pi. Звучит не очень, но на практике это куда проще.
Например, у нас есть некоторая величина X, которая принимает значения 1, 2, 5 с вероятностью 1/2, 1/4 и 1/4
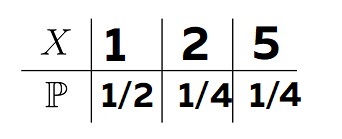
Соответственно, вероятность, что X=1 у нас будет 1/2
P(X=0) = 1/2
А вероятность, что X=10 будет 0
P(X=10) = 0
Если мы напишем в условиях x<5, то результат будет 3/4, т.к. под такое условие у нас попадает два значения
P(X<5) = 0 = 1/2 + 1/4 = 3/4
Примеры дискретных распределений
Константа. Да, это тоже случайная величина в теории вероятностей. Случайная величина X называется константой, если она принимает лишь одно значение c ∈ R с вероятностью 1
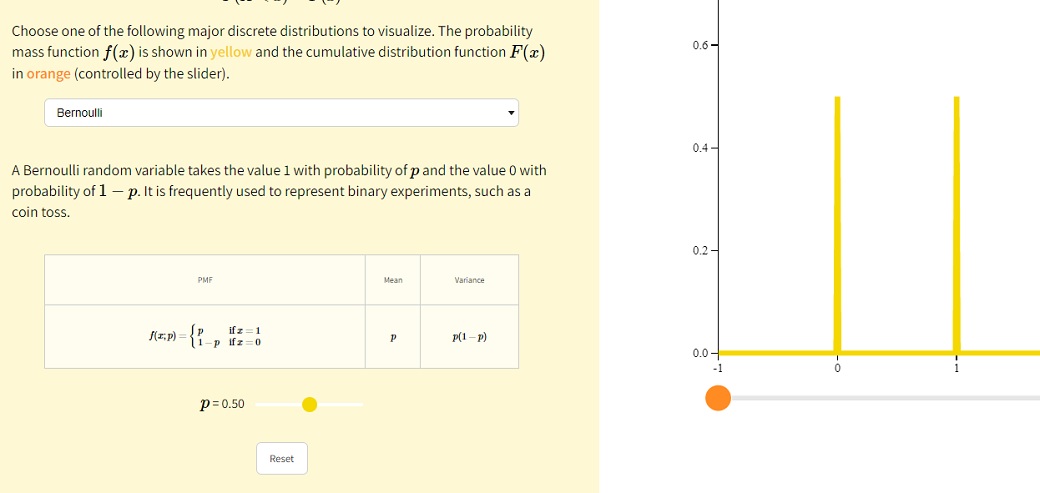
Распределение Бернулли, p ∈ [0, 1]
Самое простое распределение. То самое подбрасывание монетки, где у нас есть всего два исхода (то, что монетка может упасть ребром, мы не рассматриваем). Обозначается Ber(p). Имеет параметр p ∈ [0, 1], где p — вероятность успеха.
Случайная величина X имеет распределение Бернулли с параметром p ∈ [0, 1], если X принимает значение 1 с вероятностью p и значение 0 с вероятностью 1 − p. Параметр p называется вероятностью успеха
Таблица распределения:
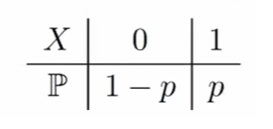
Пишется как: X ∼ Ber(0.5) — это как раз про монетку, X ∼ Ber(1).
Примеры распределения Бернулли в реальной жизни: пол сотрудника, победа спортивной команды, бумага в общественном туалете (либо она есть, либо её нет).
Равномерное распределение на конечном множестве
Случайная величина X имеет равномерное распределение на множестве {a1, a2, . . . , an}, если X принимает каждое значение ai с вероятностью 1/n. Т.е. конечное количество исходов, где каждый из них принимается с одинаковой вероятностью. Таблица распределения имеет следующий вид:
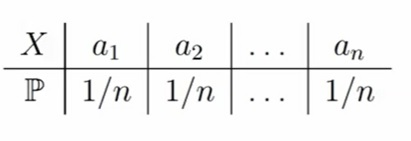
Примеры равномерного распределения в реальной жизни: игральная кость, рулетка
Биномиальное распределение Bin(n, p), n ∈ N, p ∈ [0, 1]
Здесь у нас уже два параметра. Случайная величина Y имеет биномиальное распределение с параметрами n ∈ N и p ∈ [0, 1], если Y = X1 + X2 + . . . + Xn, где X1, X2, . . . , Xn ∼ Ber(p) независимые, т.е. сумма независимых случайных величин с равностью успеха p (с одной и той же вероятностью успеха). Фактически, Y — это количество «успехов» в n независимых испытания Бернулли, от нуля до n
Примеры биномиальное распределения в реальной жизни: количество студентов, которые сдали экзамен, количество орлов в n-бросании монеты, количество кликов по ссылке у n-посетителей сайтов, количество девочек, среди n-новорожденных.
Распределение Пуассона Pois(λ), λ > 0
Параметр лямбда (λ) — это интенсивность (число больше нуля). Чем больше значение λ, тем будет больше вероятность успеха за фиксированный временной интервал (характеризует интенсивность процесса, как часто встречаются успехи в нём)
Случайная величина X имеет распределение Пуассона с параметром λ > 0, если X принимает значения k = 0, 1, 2, . . . с вероятностями:
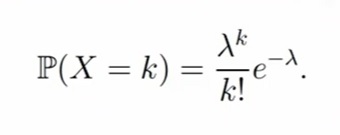
k! — факториал числа k (произведение всех натуральных чисел от 1 до k включительно)
Является предельным распределением для Bin(n, p) при p → 0, np → λ. Параметр p зависит от n. При n стремящемся к бесконечности (n -> ∞), р будет стремиться к нулю (p -> 0), но при этом np -> λ. Например, у нас есть игра «Морской бой»
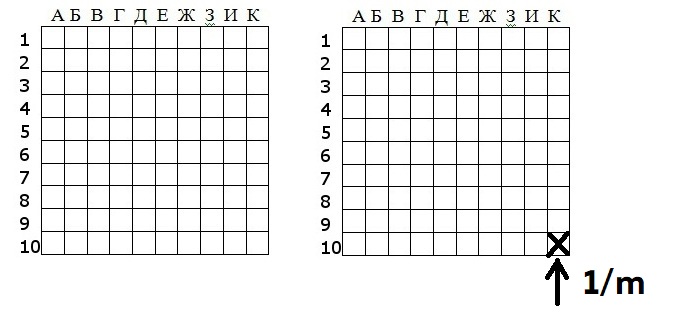
Где n- количество ходов (снарядов), а m — количество блоков. Вероятность попасть в один блок (p) будет равна 1/m. Получается биноминальное распределение с такими параметрами можно попытаться аппроксимировать с помощью распределения Пуассона

Примеры распределения Пуассона в реальной жизни: По сути, это будет количество событий, которые произошли за какой-либо временной промежуток, например: количество звонков в call-центре за час, количество рожденных детей за год
Небольшая задачка
На пустынном шоссе вероятность появления автомобиля за
30-минутный период составляет 0.95. Какова вероятность его появления
за 10 минут?
Решить её в лоб не получится, т.к.0.95 нельзя просто поделить на три — вероятность встретить автомобиль даже в случае 30 минут не равна единице, но при этом, мы можем встретить не один автомобиль, а два. Или даже три — есть множество комбинаций вероятностей.
Данная задача часто встречается на собеседованиях и интервьюеров больше интересуют ваши рассуждения о процессе решения, будете ли вы усложнять или упрощать решение.
Что сюда можно прикрутить? Условия задачи отлично подходят для распределения Бернулли. Мы можем разделить отрезок 30 минут на три равных, по 10 минут. У каждого отрезка есть случайная величина. Каждая Xi — это бернуллиевская случайная величина с вероятностью наступления успеха p
Вспоминаем таблицу распределения:
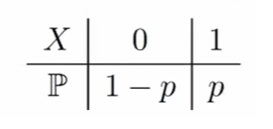
Задача сводится к том, что нам нужно найти вероятность успеха р. Получается, что нашу вероятность можно записать так:
P (Xi =1 хотя бы для одного i = 1,2,3) = 0.95
Вероятность того, что мы встретим хотя бы один автомобиль равна единице. НО! Если в событие встроено условие «хотя бы один», будет правильным перейти к дополнительному событию. Здесь мы перемножаем вероятность для xi = 0, которая равняется 1-p.
1 − P(все Xi = 0 для всех i=1,2,3) или же 1- (1-p)3
Таким образом мы получаем:
1- (1-p)3 = 0.95
В итоге, чтобы посчитать вероятность события (р), нам нужно привести формулу к такому виду:
p = 1 − 3√ 1 − 0.95
Кубический корень из 0,05 ≈ 0.37, соответственно, 1 — 0,37 = 0,67
Непрерывные случайные величины
Распределение случайных величин можно представить как распределение массы по бесконечному отрезку. При дискретном распределении мы помещали точки с какой-либо частью массы (a1, a2, a3), а саму массу делили на количество этих точек (p1,p2,p3). В общем, дискретно распределили массу в точках a1, a2, a3
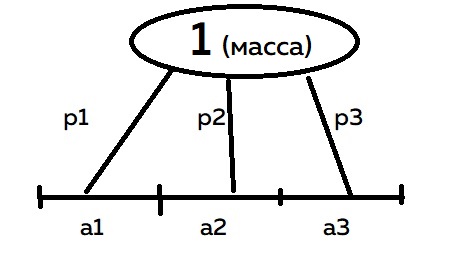
При непрерывном распределении масса будет распределяться с помощью функции плотности, которая пришла к нам из физики. Интеграл от функции плотности — это площадь под графиком. Будет это выглядеть так:
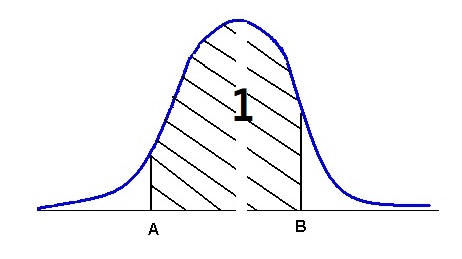
Плотность f(u) — это функция удовлетворяющая двум условиям: неотрицательность и нормировка (интеграл должен равняться единице)

Помимо этого, функция должна затухать в конце, иначе плотность будет бесконечна, а не равна единице, хвосты должны убывать
Как считать непрерывную вероятность?
Чтобы задать распределение непрерывной случайной величины X, необходимо задать функцию плотности. Если случайная величина X имеет плотность распределения f(u), то для подмножества A ⊂ R (читается как множество A является подмножеством множества R) вероятность события {X ∈ A} считается по формуле
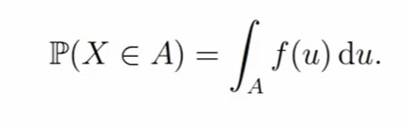
Существуют правила перехода от дискретного распределения к непрерывному: сумма по всем индексам дискретной суммы перетекает в интеграл, где ai равняется аргументу функции плотности (u), вероятности (pi) переходят в функцию плотности, умноженную на du. Например:
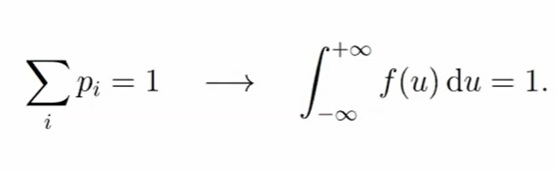
Есть нюанc: по свойствам определенного интеграла непрерывная случайная величина X с плотностью f всегда принимает наперед заданное значение a ∈ R с вероятностью 0
P(X = a) = 0
Пруф: Площадь графика от точки а до точки а будет равняться нулю, просто потому, что никакой ширины нет, то и плотности там нет никакой
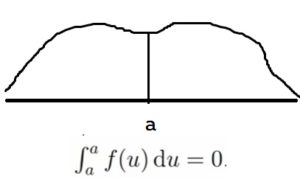
Примеры непрерывных распределений
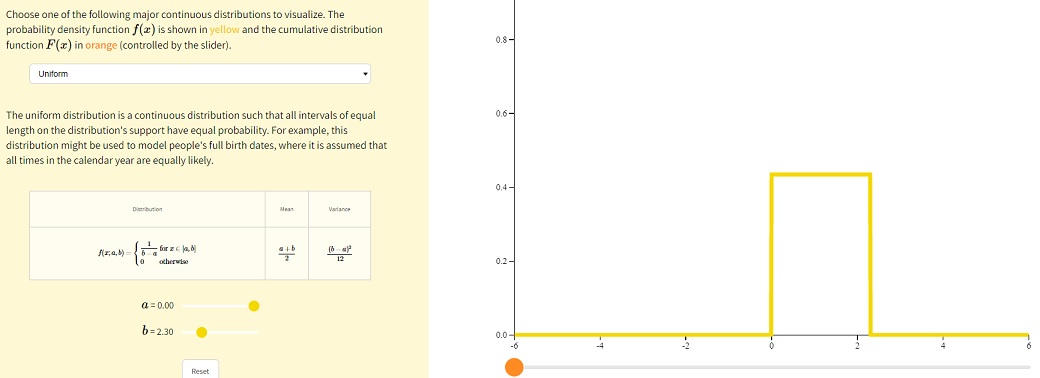
Равномерное распределение на отрезке Unif[a, b], a < b.
Равномерное распределение обозначается словом Unif (от слова uniform). По сути, это означает, что вы (по аналогии с отрезком в начале блока про непрерывные распределения) равномерно распределили массу.
Случайная величина X имеет равномерное распределение на отрезке [a, b], если её плотность f(u) имеет вид:
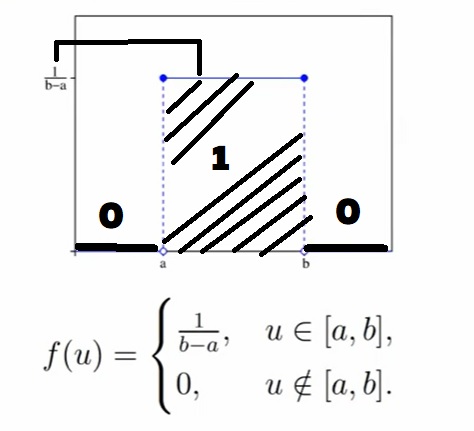
Примеры равномерного распределения из реальной жизни: Угол поворота стрелки в «Поле Чудес», генераторы (псевдо)случайных чисел, угол выстрела теннисной пушки

Экспоненциальное распределение Exp(λ), λ > 0
Случайная величина X имеет экспоненциальное (показательное) распределение с параметром λ > 0, если её плотность имеет вид:
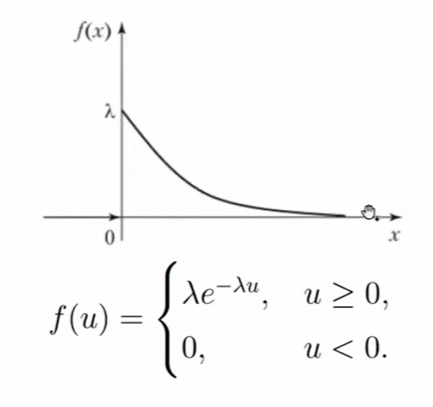
До нуля у нас будет значение 0, а уже от 0 — экспоненциальное убывание. Чем больше параметр λ, тем функция плотности убывает быстрее.
Примеры экспоненциального распределения в реальной жизни: время до приезда метро, время между покупками в «Пятерочке», срок эксплуатации какой-либо техники, время работы лампочки до перегорания.
Нормальное распределение N (µ, σ2), µ ∈ R, σ > 0
Буквы в параметрах следует читать так: µ — мю, σ — сигма. Случайная величина X имеет стандартное нормальное распределение (или стандартное гауссовское), если её плотность имеет вид:
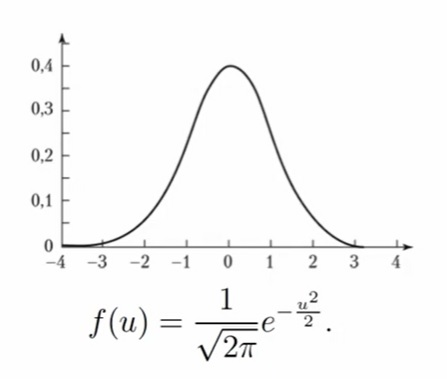
Её можно привести к такому виду:
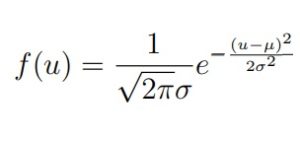
Обозначение: X ∼ N (0, 1)
В общем случае Y имеет нормальное распределение (или гауссовское) c параметрами µ ∈ R и σ > 0, если Y = µ + σX, где X ∼ N (0, 1). Изменение параметра X растягивает, либо сжимает функцию плотности. Салатовым, по центру, мы видим стандартное нормальное распределение
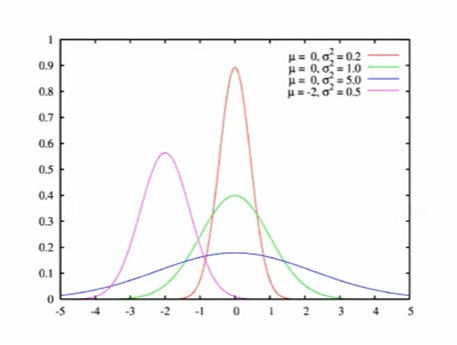
Примеры нормального распределения в реальной жизни: отклонение от среднего роста призывников, отклонения от удара футболиста при пенальти (в ворота будет приходить основная часть ударов, но будут и удары мимо — там функция будет затухать)

Визуализация дискретных и непрерывных распределений
В сети есть прекрасный сайт для визуализации распределений с подстановкой параметров. С его помощью принцип распределения становится чуть более понятным — https://seeing-theory.brown.edu/
Заходим в «Probability Distributions» и выбираем «Discrete and Continuous»
Далее можно выбрать нужное распределение и подставить параметры.
Дискретное, Бернуллевское:
Равномерное, непрерывное: